本文是关于使用 PyTorch 手动实现一个简单的线性回归的模型
仅使用 Tensor 和 autograd 实现, 适合 PyTorch 入门选手.
导入所需模块
1
2
3
4
5
6
7
| import torch
import numpy as np
import random
from IPython import display
from matplotlib import pyplot as plt
import matplotlib_inline
|
生成数据
首先我们都知道, 线性模型应该是满足如下线性函数的:
\[
f(\mathbf{x};\mathbf{w},b) = \mathbf{w}^T\mathbf{x}+b
\]
那么我们可以通过自定义权重向量 \(\mathbf{w}\) 和偏置 \(b\) 来生成我们的线性模型数据.
假设真实权重 \(\mathbf{w} = [4.5, -1.7]\), 真实偏差 \(b = 2.8\), 以及一个随机噪声 \(\epsilon\) 来确定一个训练数据集 \(\mathcal{D} = \{\mathbf{X},Y\}^{1000 \times 2}\).
1
2
3
4
5
6
7
8
| num_inputs = 2
num_examples = 1000
true_w = [4.5, -1.7]
true_b = 2.8
features = torch.tensor(np.random.normal(0,1,(num_examples,num_inputs)),dtype=torch.float)
labels = true_w[0]*features[:,0] + true_w[1]*features[:,1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),dtype=torch.float)
|
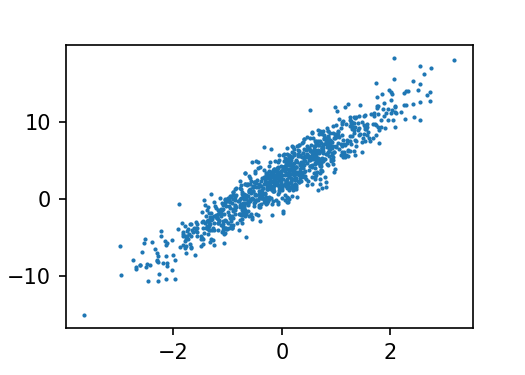
可视化查看数据的大致分布, 这里根据设置的w数据, 查看 feature0 与 label 的关系(黑暗的阅读模式下看不见坐标轴).
需要注意的是✋: 线性模型并不一定是一条线, 还有可能是一个面, 以及更高维度的表示, 所以此处的二维散点图并不能说明很多东西.
1
2
3
4
5
6
7
8
9
10
11
12
| def use_svg_display():
matplotlib_inline.backend_inline.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5,2.5)):
use_svg_display()
plt.rcParams['figure.figsize'] = figsize
set_figsize()
plt.scatter(features[:,0].numpy(), labels.numpy(), s=1)
|
读取数据集
因为我们需要多次遍历数据集, 并不断小批量的读取数据样本, 所以这里定义一个生成器函数来不断取出小批量样本.
并且我们需要随机选取数据, 所以我们借助一个等长的 list, 并使用 shuffle 打乱顺序.
1
2
3
4
5
6
7
8
| def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
j = torch.LongTensor(indices[i:min(i+batch_size, num_examples)])
yield features.index_select(0, j), labels.index_select(0, j)
|
构建模型
简单线性模型的表达形式十分简单! 利用 torch.mm 实现对 Tensor 矩阵乘法计算.
1
2
3
|
def linreg(X, w, b):
return torch.mm(X,w)+b
|
初始化模型参数
在模型训练之前, 需要对模型参数进行初始化, 权重 w 初始化为均值为 0, 标准差为 0.01 的正态分布, 偏置 b 初始化为 0.
1
2
3
|
w = torch.tensor(np.random.normal(0,0.01,(num_inputs,1)),dtype=torch.float32)
b = torch.zeros(1,dtype=torch.float32)
|
因为模型需要对参数不断的求导来获取梯度, 所以参数需要设置为可导的.
1
2
| w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
|
定义损失函数和优化算法
损失函数选择简单的平方损失函数:
\[
loss = \frac{1}{N} \sum^{N}_{n=1}(y_i-\hat{y}_i)^2
\]
1
2
3
4
|
def squared_loss(y_hat, y):
return (y_hat - y.view(y_hat.size()))**2/2
|
优化算法选择小批量梯度下降算法, 算法每次迭代时, 随机选取一小部分训练样本来计算梯度:
1
2
3
4
|
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size
|
自动求梯度模块 .grad 是求批量样本的梯度和,所以需要除去批量 size 获得梯度均值.
训练模型
接下来就开始训练模型, 需要设置小批量梯度下降的学习率 lr 和批次大小 batch_size, 以及训练轮次 num_epochs.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| lr = 0.03
num_epochs = 30
batch_size = 5
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X,w,b), y).sum()
l.backward()
sgd([w,b], lr, batch_size)
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch+1}, loss {train_l.mean().item()}')
|
最后让我们来查看一下结果, 可以发现, 模型的拟合效果还是棒棒哒👍!
1
2
3
4
5
| print(f'true_w:{true_w}, w: {w.tolist()}')
print(f'true_b:{true_b}, b: {b.tolist()}')
|
个人收获
本文学习了如何只使用PyTorch的 Tensor 数据结构和 autograd 功能, 来搭建一个非常简单的线性回归模型.
相比于之前直接使用 sklearn 来调用线性模型更有学习感, 将其中的内容更加深入的理解了, 而且学习到了一套深度学习的代码流程. 模型虽然十分简单, 不过正是一个入门 PyTorch 和深度学习的很好开始, 继续加油!
