本文是关于周志华老师编写的机器学习书籍『西瓜书』的第三章线性模型.
主要的内容有: 线性回归的基本形式、最小二乘法、广义线性回归、对数几率回归(逻辑回归)、最大似然估计、线性判别分析、广义瑞利商、拉格朗日乘子法等.
3.1 基本形式
线性模型(linear model)是一个通过属性的线性组合来进行预测的函数, 形如:
\[ f(x) = w_{1}x_{1} + x_{2}w_{2} + \dots + w_{d}x_{d} + b \]
其中\(x_i\)表示第\(i\)个属性值.
容易发现, 每个\(w_i\)都表示了属性的权重, 这使得建立的模型有很好的可解释性(comprehensibility).
一般可以写成向量形式:
\[ f(x) = \boldsymbol{w}^{T}\boldsymbol{x} + b \]
那么我们的目的就是学习得到\(\boldsymbol{w}\)和\(b\)来确定模型.
3.2 线性回归
线性回归是来学习一个线性模型, 来预测连续值. 使得预测的连续值\(f(x_i)\)尽可能是与真实值\(y_i\)接近, 即, 使得\(f(x_i) \approxeq y_{i}\).
最小二乘法
那么我们如何来衡量\(f(x_i)\)与\(y_i\)之间的差距呢, 这时候可以上文提过的均方误差(MSE)来衡量\(f(x_i)\)与\(y_i\)之间的差距. 并使其最小化, 就可以得到我们先想要的\(\boldsymbol{w}\)和\(b\):
\[ \begin{aligned} (w^*, b^*) &= \argmin_{(\boldsymbol{w}, b)}{\sum^m_{i=1}{(f(x_i)-y_i)^2}} \\ &= \argmin_{(\boldsymbol{w}, b)}{\sum^m_{i=1}{(y_i-wx_i-b)^2}} \end{aligned} \]
这就是最小二乘法(least square method): 使用均方误差这个具有几何意义的欧氏距离来度量差距.
OK, 那么我们下一步就是如何求解\(E_{(w,b)}= {\sum^m_{i=1}{(y_i-wx_i-b)^2}}\)最小值了, 这一步叫做最小二乘的参数估计(parameter estimate), 对\(\boldsymbol{w}\)和\(b\)和b分别求偏导, 并令为零可以得到\(\boldsymbol{w}\)和\(b\)的最优解:
\[ w = \frac{\sum\limits^m_{i=1}{y_i(x_i-\bar{x})}}{\sum\limits^m_{i=1}{x_i^2}-\frac{1}{m}(\sum\limits^m_{i=1}{x_i})^2} \]
\[ b = \frac{1}{m}\sum^m_{i=1}{(y_i-wx_i)} \]
矩阵形式
当我们将数据扩展为矩阵形式, 把\(\boldsymbol{w}\)和\(b\)写入向量形式\(\boldsymbol{w} = (\boldsymbol{w}, b)\), 相应地, 把数据集\(D\)表示为一个\(m*(d+1)\)大小的矩阵\(\boldsymbol{X}\), 其中每一行代表一个实例,每行前d个元素对应实例中的d个属性, 最后一个元素恒为1. \[ \boldsymbol{X} = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1 \\ \vdots & \vdots & & \vdots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{md} & 1 \\ \end{pmatrix} = \begin{pmatrix} \boldsymbol{x_1}^T & 1 \\ \boldsymbol{x_2}^T & 1 \\ \vdots & \vdots \\ \boldsymbol{x_m}^T & 1 \\ \end{pmatrix} \]
再将输入也写成向量形式
\[ \boldsymbol{y} = (y_1, y_2, \cdots, y_m) \]
根据均方差误差最小化原则有:
\[ \boldsymbol{w}^\ast = arg \min_w(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w})^T(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}) \]
令\(\boldsymbol{E_w} = (\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w})^T(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w})\), 对\(\boldsymbol{w}\)求导得到
\[ \frac{\partial\boldsymbol{E_w}}{\partial\boldsymbol{w}} = 2\boldsymbol{X}^{T}(\boldsymbol{X}\boldsymbol{w}-\boldsymbol{y}) \]
令其为零可得到\(\boldsymbol{W}\)的最优解的闭式解。
以上是当矩阵\(X^TX\)满秩(可逆)时进行的计算, 而实际中, 很多的数据矩阵是非满秩的, 则有可能会解出多个解, 那么选择解由学习算法的归纳偏好决定, 常见做法是引入正则化.
广义线性回归
以上我们针对的是一个简单线性回归的模型, 显然预测得到的标记一定是一个线性的结果.
此时我们实验中获得了一组数据, 通过观察是符合指数函数形式的, 很明显是一个非线性的标记序列, 那这时是否可以使用线性回归呢?
答案是可以的.
我们对标记\(y\)取ln函数, 这时就会发现:
\[ \ln{y} = \boldsymbol{w}^{T}\boldsymbol{x} + b \]
这就是对数线性回归, 在形式上我们可以使用线性回归进行表示, 但本质上却实现了非线性回归. 发生这时神奇变化的东西就是ln这个单调可微函数.
由此推到广义线性模型(generalized linear model), 使用单调可微函数\(g(\cdot)\)来将预测值和实际值联系起来.
\[ y = g^{-1}(\boldsymbol{w}^{T}\boldsymbol{x} + b) \]
3.3 对数几率回归
对数几率回归也就是我们之前经常听说的逻辑回归. 但是逻辑(logistic)其实并不合适, 而对数几率(log odds, logit)才是这个模型的本质, 下面详细介绍.
我们在上面所提到的广义线性回归中, 使用一个特定的函数来代替单调可微函数\(g^{-1}(\cdot)\)——sigmoid函数.
\[ y = \frac{1}{1+e^{-z}} \]
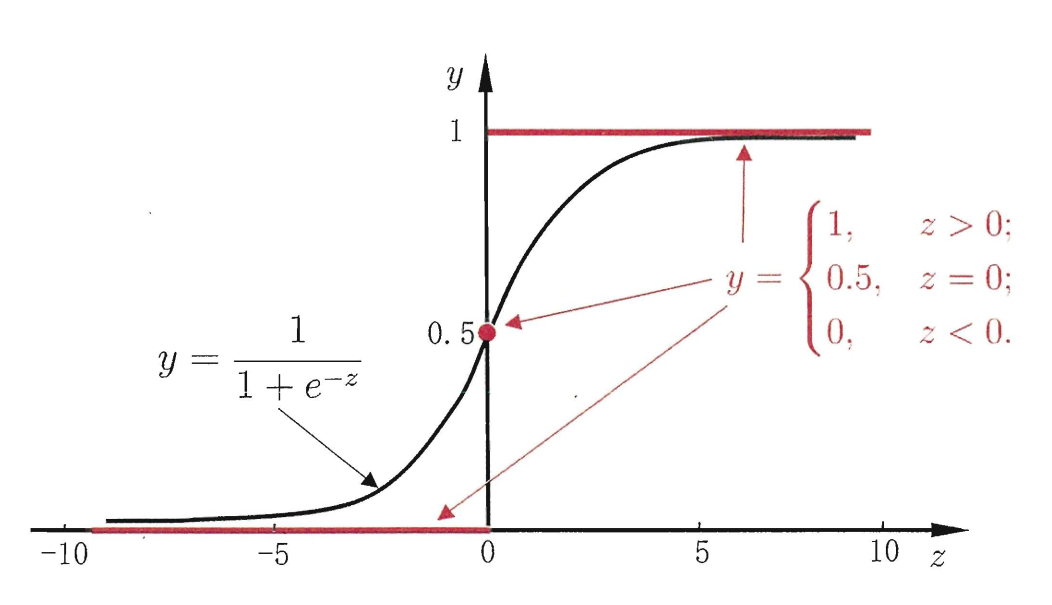
这是一个形如s型曲线的图像, 通过设置不同的阈值, 使得取值被划分为0或1, 所以这也是为什么虽然叫做回归函数, 却经常被用作分类.
模型的表示(模型)
将线性模型带入sigmoid函数中, 可以得到:
\[ y = \frac{1}{1+e^{-(\boldsymbol{w}^{T}\boldsymbol{x} + b)}} \]
通过变化得到:
\[ \ln{\frac{y}{1-y}} = \boldsymbol{w}^{T}\boldsymbol{x} + b \]
此时很关键的一步:
- 将\(y\)视作样本\(\boldsymbol{x}\)为正例的可能性, 用后验概率表示为\(p(y=1|\boldsymbol{x})\);
- 将\(1-y\)视作样本\(\boldsymbol{x}\)为反例的可能性, 用后验概率表示为\(p(y=0|\boldsymbol{x})\).
我们所谓的"几率"就是\(\frac{y}{1-y}\), 反映了x作为正例的相对可能性. 再取对数, 所以就称为对数几率!
最大似然估计(策略)
那么问题回到如何确定模型中的\(\boldsymbol{w}\)和\(b\)呢? 我们这里使用最大似然估计来解释, 同样的还可以使用信息论的角度来解释.
根据以上的内容, 可以将模型表达写成:
\[ p(y=1|\boldsymbol{x}) = \frac{e^{\boldsymbol{w}^{T}\boldsymbol{x} + b}}{1+e^{\boldsymbol{w}^{T}\boldsymbol{x} + b}} \]
\[ p(y=0|\boldsymbol{x}) = \frac{1}{1+e^{\boldsymbol{w}^{T}\boldsymbol{x} + b}} \]
通过极大似然估计法, 并取对数就可以得到:
\[ \begin{aligned} L(\boldsymbol{w}, b) &= \prod^m_{i=1}{p(y_i|\boldsymbol{x}_i;w,b)} \\ l(\boldsymbol{w}, b) &= \sum^m_{i=1}{\ln{[y_ip_1(\hat{\boldsymbol{x}}_i;\boldsymbol{w}, b) + (1-y_i)p_0(\hat{\boldsymbol{x}}_i;\boldsymbol{w}, b)]}}\end{aligned} \]
其中\(p_1\)是\(p(y=1|\boldsymbol{x};\boldsymbol{w}, b)\), \(p_0\)是\(p(y=0|\boldsymbol{x};\boldsymbol{w}, b)\).
为了便于讨论, 令\(\beta=(\boldsymbol{x};b), \hat{\boldsymbol{x}}=(\boldsymbol{x};1)\), 使得\(\boldsymbol{w}^{T}\boldsymbol{x} + b\)可以表示为\(\beta^T\boldsymbol{x}\). 再分别令\(y_i\)为0或1:
\[ l(\beta) = \begin{cases} \sum\limits^m_{i=1}{- \ln{(1+e^{\beta^T\boldsymbol{x}_i})}}, \qquad &y_i = 0 \\ \sum\limits^m_{i=1}{\beta^T\boldsymbol{x}_i - \ln{(1+e^{\beta^T\boldsymbol{x}_i})}}, \qquad &y_i = 1 \end{cases} \]
综合可得如下式子, 并且将其取负数得最小化:
\[ l(\beta) = -\sum^m_{i=1}{[y_i\beta^T\boldsymbol{x}_i - \ln{(1+e^{\beta^T\boldsymbol{x}_i})}]} \]
这就是关于\(\beta\)的高阶可导凸函数, 使用梯度下降等优化理论方法进行求解即可.
模型的优点
- 该模型直接对分类的可能性进行建模, 也没有要求数据分布, 避免假设数据分布带来的不确定性问题;
- 而且得到了近似概率预测, 对许多需要利用概率辅助决策的任务有很大的帮助;
- 求解的目标函数是任意阶可导的凸函数, 有很好的数学性质, 许多值优化算法都可以用来求解最优解.
3.4 线性判别分析
线性判别分析(linear Discrimination Analysis, LDA)是一种典型的二分类方法.
主要思想是: 在给定的训练样本集中, 试图寻找一条直线, 并让所有的样本点投影到该直线上, 其中同类样本点的投影之间尽可能的接近, 异类样本点的投影之间尽可能远离.当需要对新样本进行分类时, 同样将新样本投影到该直线上, 根据其位置判断属于哪一类.
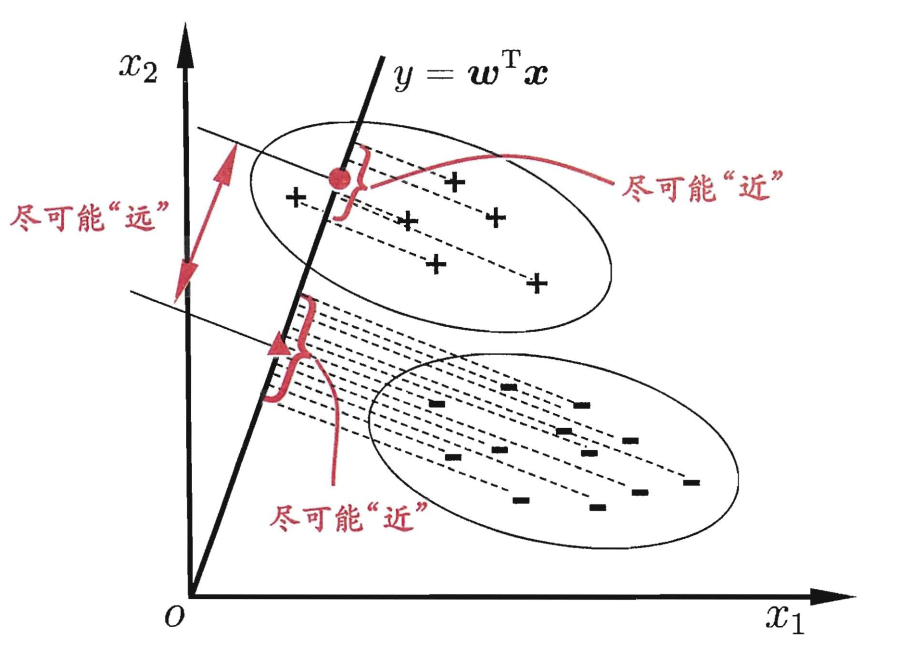
针对二分类问题(模型)
接下来, 首先对一些符号进行说明. 数据集: \(D=\{(\boldsymbol{x}_i,y_i)\}^m_{i=1}\), 其中标记取值为0或1: \(y_i=\{0,1\}\), 第\(i=\{0, 1\}\)类示例的集合为\(X_i\), 均值向量为\(\mu_i\), 协方差矩阵为\(\Sigma_i\).
协方差矩阵\(\Sigma\)(读
Sigma)与求和符号\(\sum\)(读sum)还是不一样的,注意通过上下文进行区分.协方差矩阵表示的是各个属性之间的相关性, 为0表示不相关. 因此协方差矩阵的大小与属性的个数有关, 而与样本的个数无关.
根据以上对符号的定义,
- 将样本点投影到直线上得到: \(\boldsymbol{w}^T\mu_0\) 和 \(\boldsymbol{w}^T\mu_1\);
- 将所有样本点投影到直线上得到两类样本的协方差为: \(\boldsymbol{w}^T\Sigma_0\boldsymbol{w}\) 和 \(\boldsymbol{w}^T\Sigma_1\boldsymbol{w}\).
由于我们的目的是使得两类样本之间的距离尽可能的大, 而样本内的距离尽可能的小, 那么就需要使得\(\|\boldsymbol{w}^T\mu_0 - \boldsymbol{w}^T\mu_1\|^2_2\)尽可能的大, 而\(\boldsymbol{w}^T\Sigma_0\boldsymbol{w} + \boldsymbol{w}^T\Sigma_1\boldsymbol{w}\)尽可能的小.
\(\|X\|^2_2这叫做二范数的平方, 表示向量之间的距离, 可以使用向量的内积进行计算\)
我们需要注意 ⚠ ! 我们的目的是为了求出投影直线的方向, 所以\(\boldsymbol{w}\)的大小无关紧要, 这也是下面很多步骤中的必要条件.
损失函数(策略)
同时考虑以上两者, 可以得到我们的最大化目标:
\[ \begin{aligned} \max J &= \frac{\|\boldsymbol{w}^T\mu_0 - \boldsymbol{w}^T\mu_1\|^2_2}{\boldsymbol{w}^T\Sigma_0\boldsymbol{w} + \boldsymbol{w}^T\Sigma_1\boldsymbol{w}} \\ &= \frac{\|(\mu_0-\mu_1)^T\boldsymbol{w}\|^2_2}{\boldsymbol{w}^T(\Sigma_0+\Sigma_1)\boldsymbol{w}} \\ &= \frac{w^T (\mu_0-\mu_1)(\mu_0-\mu_1)^T \boldsymbol{w}}{\boldsymbol{w}^T(\Sigma_0+\Sigma_1)\boldsymbol{w}} \end{aligned} \]
并定义"类内散度矩阵"(within-class scatter matrix): \(\boldsymbol{S}_w = \Sigma_0 + \Sigma_1\), "类间散度矩阵"(between-class scatter matrix): \(\boldsymbol{S}_b = (\mu_0-\mu_1)(\mu_0-\mu_1)^T\).
那么上式可以表示为:
\[ \max J = \frac{\boldsymbol{w}^T \boldsymbol{S}_b \boldsymbol{w}}{\boldsymbol{w}^T \boldsymbol{S}_w \boldsymbol{w}} \]
以上这个最大化的目标函数其实就是\(\boldsymbol{S}_b\)与\(\boldsymbol{S}_w\)的"广义瑞利商".
并注意到我们需要求解的\(\boldsymbol{w}\)只与方向有关, 而与大小无关, 那么不失一般性的, 可以令分母\(\boldsymbol{w}^T \boldsymbol{S}_w \boldsymbol{w}=1\), 由此等价于:
\[ \begin{aligned} \min_{\boldsymbol{w}}\quad&{-\boldsymbol{w}^T \boldsymbol{S}_b \boldsymbol{w}} \\ s.t. \quad &\boldsymbol{w}^T \boldsymbol{S}_w \boldsymbol{w}=1 \end{aligned} \]
拉格朗日乘子法(求解)
关于这种仅含有等式约束的问题, 可以使用拉格朗日乘子法进行求解.
即, 可得:
\[ L(\boldsymbol{w}, \lambda) = -\boldsymbol{w}^T \boldsymbol{S}_b \boldsymbol{w} + \lambda(\boldsymbol{w}^T \boldsymbol{S}_w \boldsymbol{w} - 1) \]
再对\(\boldsymbol{w}\)求偏导可得:
\[ \frac{\partial{L(\boldsymbol{w}, \lambda)}}{\partial{\boldsymbol{w}}} = -(\boldsymbol{S}_b+\boldsymbol{S}_b^T)\boldsymbol{w} + \lambda(\boldsymbol{S}_w+\boldsymbol{S}_w^T)\boldsymbol{w} \]
令等式为0可得:
\[ \boldsymbol{S}_b\boldsymbol{w} = \lambda\boldsymbol{S}_w\boldsymbol{w} \]
因为\((\mu_0-\mu_1)^T\boldsymbol{w}\)为实数, 所以\(\boldsymbol{S}_b\boldsymbol{w} = (\mu_0-\mu_1)(\mu_0-\mu_1)^T\boldsymbol{w}\)的方向恒为\((\mu_0-\mu_1)\), 所以可以解得:
\[ \boldsymbol{w} = \boldsymbol{S}^{-1}_w(\mu_0-\mu_1) \]
可以发现, 我们求得的\(\boldsymbol{w}\)的值, 就是\(\boldsymbol{S}_b\)对应于\(\boldsymbol{S}_b\)的广义特征值对应的特征向量
多分类问题
而多分类的问题中, 只不过是求矩阵\(\boldsymbol{W}\), 使得\(\boldsymbol{S}_b\boldsymbol{W} = \lambda\boldsymbol{S}_w\boldsymbol{W}\).
我们将\(\boldsymbol{W}\)拆分为多个二分类问题可得: \(\boldsymbol{W} = \{\boldsymbol{w}_1, \boldsymbol{w}_1, \dots, \boldsymbol{w}_n\}\), 结合广义特征值与广义瑞利商的性质可以得到\(\boldsymbol{W}\)其实就是\(\boldsymbol{S}_b\)相对于\(\boldsymbol{S}_w\)最大的非零广义特征值所对应的特征向量组成的矩阵!
个人收获
- 从单纯的线性模型, 推广到广义的线性模型, 再引出特殊的对数几率回归模型. 从特殊到一般再到特殊的方式, 很好的理清楚了简单线性回归和逻辑回归之间的关系.
- 逻辑回归真正的名字应该是对数几率回归, 这对记忆和理解模型都有更好的可解释性.
- 线性判别分析法这次终于学明白了! 从"模型-策略-求解"三方面进行学习果然思路清楚了很多.
- 公式的推导依旧有难度, 目前处于抛开书想不到怎么推, 但结合西瓜书和南瓜书还是能够看懂推导过程.
继续加油!